При нахождении однозначных выражений числа под корнем мы ищем такие выражения, которые при подстановке чисел образуют квадрат данного числа. Это позволяет нам найти решения уравнений или упростить выражения, содержащие корень.
Метод замены переменной
Принцип работы метода замены переменной
Основная идея метода замены переменной заключается в том, что мы заменяем исходную переменную на новую переменную, таким образом, что новое уравнение становится проще для решения. Зачастую, для этого используется подход, где мы заменяем подкоренное выражение на новую переменную.
Пример подкоренного выражения: √(x 2 + 1). Мы можем заменить x 2 + 1 на новую переменную — y, и таким образом упростить исходное уравнение.
Процесс решения уравнения с использованием метода замены переменной
- Определить подкоренное выражение в исходном уравнении.
- Заменить подкоренное выражение на новую переменную.
- Исследовать и преобразовать уравнение с учетом новой переменной.
- Решить полученное уравнение и найти значения новой переменной.
- Подставить найденные значения новой переменной обратно в исходное уравнение и найти значения исходной переменной.
Пример решения уравнения с использованием метода замены переменной
Рассмотрим пример уравнения √(x 2 + 1) — x = 2 и применим метод замены переменной:
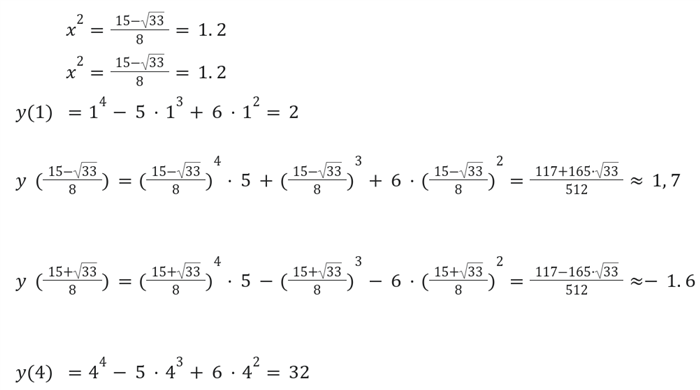
- Подкоренное выражение: x 2 + 1
- Заменяем x 2 + 1 на новую переменную y.
- Уравнение примет вид: √y — x = 2
- Решаем новое уравнение √y — x = 2 относительно переменной y.
- Находим значение новой переменной: y = (x + 2) 2
- Подставляем значение y = (x + 2) 2 в исходное уравнение и решаем его относительно переменной x.
- Находим значения исходной переменной: x = -1 и x = 3.
Метод замены переменной является мощным инструментом при решении уравнений, особенно при нахождении подкоренных выражений. Замена переменной позволяет упростить уравнение, что делает его более подходящим для решения и облегчает процесс нахождения корней. Учитывая его простоту и эффективность, метод замены переменной стоит усвоить и использовать при решении уравнений.
Область определения показательной и логарифмической функции
Показательная функция
Показательная функция имеет вид f(x) = a x, где a — положительное число и a ≠ 1. Она описывает экспоненциальный рост или убывание, где a определяет скорость изменения значения функции.
Область определения показательной функции включает все действительные числа x. Это означает, что выражение a x определено для любого вещественного числа и не имеет ограничений на входные параметры.
Логарифмическая функция
Логарифмическая функция задается формулой f(x) = loga(x), где a — положительное число и a ≠ 1. Она является обратной функцией к показательной функции и позволяет найти показатель, с которым число a должно быть возведено, чтобы получить число x.
Область определения логарифмической функции определяется положительными действительными числами x, так как логарифм не определен для отрицательных чисел и нуля.
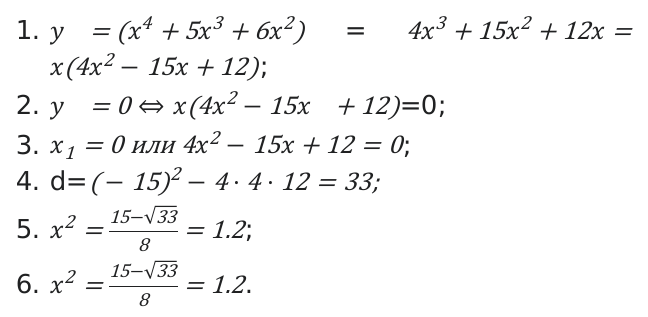
Свойства показательной и логарифмической функции
Показательная и логарифмическая функции обладают следующими свойствами:
- Показательная функция с положительным основанием a всегда принимает положительные значения, кроме случая a = 1, когда f(x) = 1 для любого x.
- Логарифмическая функция с положительным основанием a возвращает только положительные значения для положительных входных параметров.
- Пересекаясь с осью абсцисс (x-осью), показательная функция имеет горизонтальную асимптоту в точке y = 0.
- Пересекаясь с осью ординат (y-осью), логарифмическая функция имеет вертикальную асимптоту в точке x = 0.
Применение показательной и логарифмической функций
Показательная и логарифмическая функции широко применяются в научных и инженерных исследованиях, а также в различных практических задачах. Некоторые из областей применения включают:
- Финансовая математика и экономика, где показательная функция используется для моделирования экономического роста и денежных потоков.
- Физика и естественные науки, где показательная и логарифмическая функции помогают описывать процессы развития и распада.
- Компьютерные науки и информационные технологии, где логарифмическая функция используется для измерения сложности алгоритмов и эффективности программ.
- Статистика и вероятность, где показательная и логарифмическая функции используются для моделирования случайных процессов и распределений.
Метод уединения радикала в теории чисел
Принцип метода
Метод уединения радикала базируется на следующем принципе: если в сложном математическом выражении присутствует корень, то можно изолировать данный корень, переведя его в отдельный множитель. Таким образом, можно выделить из исходного выражения простые радикальные выражения, что упрощает последующие вычисления и анализ.
Пример применения метода
Рассмотрим пример применения метода уединения радикала. Предположим, у нас имеется следующее выражение:
√(12 + 3√7 — 4√3)

С помощью метода уединения радикала мы можем разбить данное выражение на три отдельных множителя:
- √12
- √7
- √3
Далее, мы можем привести каждый множитель к более простому виду:
- √(2 2 * 3)
- √7
- √3
Используя свойства корня, мы можем упростить выражение до следующего вида:
- 2√3
- √7
- √3
Таким образом, мы получили однозначное выражение числа под корнем, которое можно использовать в дальнейших вычислениях или анализе.
Метод уединения радикала является полезным инструментом в теории чисел для упрощения сложных выражений с корнями. Он позволяет разделить такие выражения на более простые, что делает дальнейшие математические операции более удобными и понятными. Применение метода уединения радикала требует некоторого опыта и знаний в области работы с корнями, но при правильном использовании он может быть очень эффективным инструментом в решении математических задач.
Как найти ОДЗ?
Шаги по нахождению ОДЗ:
- Определите тип переменной: действительные числа, натуральные числа, целые числа.
- Изучите условие задачи или уравнения, чтобы определить ограничения на переменную.
- Проверьте наличие исключений, при которых ОДЗ может быть ограничено или не существовать.
- Проанализируйте все условия на переменную и определите интервалы, в которых она может находиться.
- Запишите ОДЗ в виде интервалов, промежутков или множеств.
Примеры нахождения ОДЗ:
Пример 1:
Найти ОДЗ уравнения: √(5x — 7) = 2.
- Переменная x должна быть действительным числом.
- Условие задачи: корень из выражения (5x — 7) должен равняться 2.
- Исключений нет.
- Выражение под корнем должно быть неотрицательным: 5x — 7 ≥ 0.
- Найдите ОДЗ: x ≥ 7/5.
Пример 2:
Найти ОДЗ уравнения: log₂(3x + 4) > 2.
- Переменная x должна быть действительным числом.
- Условие задачи: логарифм выражения (3x + 4) по основанию 2 должен быть больше 2.
- Исключений нет.
- Выражение под логарифмом должно быть положительным: 3x + 4 > 0.
- Найдите ОДЗ: x > -4/3.
Нахождение ОДЗ является важным шагом в решении задач и уравнений. Правильное определение ОДЗ позволяет избежать ошибок при проведении математических операций и обеспечить корректные результаты.
Область определения функции в виде дробного алгебраического значения
Важно отметить, что в дробных алгебраических значениях не допускаются деление на ноль или корень из отрицательного числа. Эти значения являются неопределенными и приводят к математической ошибке или несуществованию.
Ограничения и условия для области определения
Для определения области определения функции в виде дробного алгебраического значения, необходимо учитывать следующие ограничения и условия:
- Деление на ноль не допускается: знаменатель дроби не может равняться нулю. Если знаменатель равен нулю, то функция не имеет определенного значения.
- Избегайте отрицательных значений под корнем: если числитель или знаменатель дроби содержат отрицательные значения, то под корнем стоит отрицательное число. В таком случае функция также не будет иметь определенного значения.
- Дополнительные ограничения, указанные в задаче: в некоторых случаях могут быть указаны дополнительные ограничения, такие как значения, которые должны быть включены или исключены из области определения функции.
Примеры области определения
Давайте рассмотрим несколько примеров области определения функции в виде дробного алгебраического значения:
| Функция | Область определения |
|---|---|
| f(x) = 1 / x | Область определения: все дробные числа, кроме 0, так как деление на ноль не допускается. |
| g(x) = √(x — 4) | Область определения: все значения x, которые больше или равны 4, так как отрицательные значения под корнем не допускаются. |
| h(x) = 1 / (x + 2) | Область определения: все дробные числа, кроме -2, так как деление на ноль не допускается. |
В каждом из этих примеров область определения функции состоит из дробных чисел, удовлетворяющих определенным ограничениям и условиям. Это позволяет определить значения функции и взаимосвязь между входными и выходными данными.